The 7 types of angles, and how they can create geometric shapes
Mathematics is one of the purest and technically objective sciences that exist . In fact, in the study and research of other sciences, different procedures are used from branches of mathematics such as calculus, geometry or statistics.
In Psychology, without going any further, some researchers have proposed to understand human behavior from the typical methods of engineering and mathematics applied to programming. One of the best-known authors in proposing this approach was Kurt Lewin, for example.
In one of the aforementioned, geometry, we work from shapes and angles. These shapes, which can be used to represent areas of action, are estimated simply by opening these angles placed at the corners. In this article we are going to observe the different types of angles that exist .
- Maybe you're interested: "Psychology and statistics: the importance of probabilities in the science of behavior"
The angle
It is understood by angle to the part of the plane or portion of reality that separates two lines with the same point in common . It is also considered as such the rotation that should carry out one of its lines to go from one position to another.
The angle is formed by different elements, among which stand out the edges or sides that would be the straight lines that are related, and the vertex or point of union between them .
- Maybe you're interested: "Logical-mathematical intelligence: what is it and how can we improve it?"
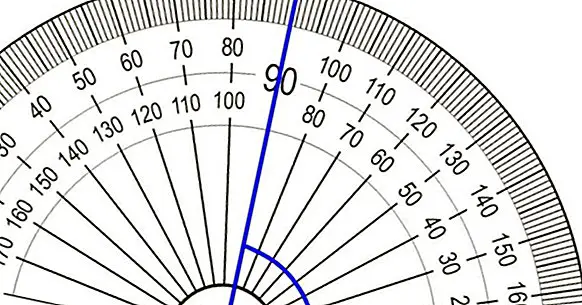
Types of angles
Below you can see the different types of angles that exist.
1. Sharp angle
It is called as such that type of angle that it has between 0 and 90 ° , not including the latter. An easy way to imagine an acute angle can be if we think of an analog clock: if we had a fixed hand pointing to twelve and the other before they were and fourth we would have an acute angle.
2. Right angle
The right angle is one that measures exactly 90 °, being the lines that are part of it completely perpendicular. For example, the sides of a square form angles of 90º to each other.
3. Obtuse angle
It is called that angle that presents between 90 ° and 180 °, without including them. If it were twelve o'clock, the angle that the hands of a clock would make between each other It would be obtuse if we had one hand pointing to twelve o'clock and the other one and a half and a half .
4. Plain angle
That angle whose measurement reflects the existence of 180 degrees. The lines that form the sides of the angle are joined in such a way that one looks like an extension of the other, as if they were a single line. If we turn our body around we will have made a 180 ° turn. On a clock, an example of a flat angle, we would see it at twelve-thirty if the hand pointing at twelve was still at twelve.
5. Concave angle
That angle of more than 180 ° and less than 360 ° . If we have a round cake in parts from the center, a concave angle would be the one that would form what remained of the cake as long as we ate less than half.
6. Full or perigonal angle
This angle concretely makes 360 °, remaining the object that realizes it in its original position. If we give a complete turn returning to the same position as at the beginning, or if we go around the world finishing exactly in the same place we started, we will have made a 360º turn.
7. Null angle
It would correspond to an angle of 0º.
Relations between these mathematical elements
In addition to the angle types, we must bear in mind that depending on the point at which the relationship between the lines is observed, we will be observing one angle or the other. For example, in the example of the cake, we can take into account the missing portion or the portion that remains of it. The angles can relate to each other in different ways , being some examples those that are shown next.
Complementary angles
Two angles are complementary if their angles add up to 90 °.
Supplementary angles
Two angles are supplementary when the result of its sum generates an angle of 180 ° .
Consecutive angles
Two angles are consecutive when they have a side and a vertex in common.
Adjacent angles
They are understood as such those consecutive angles whose sum allows to form a flat angle . For example, an angle of 60 ° and another of 120 ° are adjacent.
Opposite angles
Angles that had the same degrees but of opposite valence would be opposite.One is the positive angle and the other is the same but of negative value.
Opposite angles by the vertex
It would be two angles that they start from the same vertex by extending the rays that form the sides beyond their point of union . The image is equivalent to that which would be seen in a mirror if the reflecting surface were placed together at the vertex and then placed on a plane.